Easing and Splines Research

I am Marc Garcia, student of the Bachelor’s Degree in Video Games by UPC at CITM. This content is made for the second year’s subject Project 2, under supervision of lecturer Ricard Pillosu.

Introduction

The aim of my research is to obtain codewise a library that supports over 30 easing functions developed by the lead developer Robert Penner. Moreover I had to make a camera that follows a pre-existant spline, in which I failed resoundingly in addition of a camera that translates between two points with soft acceleration based on an easing function from my library. Even though it’s not completely functional I achieved something close to what was expected.

Easing

Easing functions allow to apply mathematical formulas like splines to certain animations in order to diminish the amount of work required for each animation which means that the function itself describes the movement instead of hardcoding it for each animation. Also, by giving the animation certain acceleration it allows the coder to achieve a much more smooth result. In the case of a camera, instead of coding the amount of distance it needs to travel each frame it gives the camera a speed depending on the distance from his objective position.

Each easing function depends on four parameters:

Current time (t) which is the moment where the object is.
Beginning value (b) which the position where the object is at the moment t.
Change in value (c) which is the difference of value between the current position and the final position.
Duration (d) which is the total number of iterations that you want your animation to have, needs to be the current unit as the starting time.

Easing functions types

There are different types of easing functions, five standard classes and some other more complex.

The six standard classes use a power that ranges from 1 to 5:

Linear using a power of 1, which means that at 20% of the tween the object will be at the 20 % of distance.
Quad using a power of 2, which means that the value would increase by a power of 2.
Cubic using a power of 3.
Quard using a power of 4.
Quint, also called Strong, using a power of 5.
Circular using a power of 6. The more the power of the function the faster it will increase its speed.

The other more complex classes apply a different Math method are:

Sinusoidal applying the mathematical cosine and sine methods
Exponential is similar to the standar classes but instead of using a power it increases/decreases exponentially to the inital value.
Elastic tries to imitate the movement of a string where it accelerates and deaccelerates smoothly.
Back allows the object to bypass the objective and then return as if there were a reverse gravity.
Bounce tries to imitate the movement of a bouncing ball, for example, applying an acceleration and deacceleration similar to the gravity would.

Moreover, each of these classes excepting the Linear which actually doesn’t have easing, include the ease in, ease out and ease in and out functions.

Ease in function describes the positive acceleration of the object.
Ease out function describes the negative acceleration (deacceleration) of the object.
Ease in and out function mixes both of the previous functions describing first and acceleration followed by a deacceleration.

Easing Usability

In computer science easing is very useful in different areas, mainly object oriented programming, 2D or 3D animation and camera views. In photoshop and other similar animation software tools there’s a curve that simulates an easing function that allows the user to define the speed over each iterations of your animation. This allows the user to avoid creating hundreds of frames for a simple movement and instead it does it automatically taking in account the distance between frame. In the case of camera views, an easing function allows the user to create a much more smooth experience and save up a lot of time by not having to hard code every step the camera needs to progress over its trajectory.

How it works?

Imagine you have an animation you need to move over a surface and in order to make it more realistic you want to add some cubic ease in to its movement. To do so you need to pass the function CubicEaseIn() 4 parameters so it would look like:

CubicEaseIn(currentTime, beginning value, distanceToGoal, totalTime);

Remember that every easing function returns a value you need to store in a variable.

float currentValue;

currentValue = CubicEaseIn(currentTime, beginningValue, distanceToGoal, totalTime);

In case your program runs at 60 frames per second and you want the animation to take a total of 5 seconds, your total time would be 300 iterations (remember the units of the current and total time must be the same in order to work). Taking this into account the function would now look like this.

float currentValue;
int totalIterations = 300;

currentValue = CubicEaseIn(currentTime, beginningValue, distanceToGoal, totalIterations);

The function above would take into account the total number of iterations but it also requires the iteration the animation is at that moment. To do that you need a variable that stores the current iteration the animation is.

float currentValue;
int totalIterations = 300;
int currentIteration = 0;

currentValue = CubicEaseIn(currentIteration, beginningValue, distanceToGoal, totalIterations);
currentIteration++

At the moment we have the function to take into account the time it needs to run at every moment. Imagining we want an horizontal translation where the first point is at x=100 and the final value at x= 750, we need to variables that store its position to be able to import it from an XML if we wish so. As the second variable would store the distance it would look like something like this:

float currentValue;
int totalIterations = 300;
int currentIteration = 0;
int firstPoint = 100;
int secondPoint = 750;
int distanceBetweenPoints = secondPoint - firstPoint;

currentValue = CubicEaseIn(currentIteration, firstPoint, distanceBetweenPoints, totalIterations);
currentIteration++

This would now return the exact speed the camera needs at every frame to get from one point to another. But it needs to be reset when achieving the total number of iterations to not have an infinite easing through a bool that specifies if you want an easing or not that can be activated by any condition.

float currentValue;
bool easingActive;
int totalIterations = 300;
int currentIteration = 0;
int firstPoint = 100;
int secondPoint = 750;
int distanceBetweenPoints = secondPoint - firstPoint;

if (yourCondition){
	easingActive = true;
}
if (easingActive){
	currentValue = CubicEaseIn(currentIteration, firstPoint, distanceBetweenPoints, totalIterations);
}
if (currentIteration < totalIterations {
	currentIteration++
}
else {
	currentIterations = 0;
	easingActive = false;
}

This piece of code would now fill the currentValue with your speed at each moment so you just need to add this value to the position of your object in order to do the easing.

Video example of its functionality:

Easing functions graphics and code

The following graphs will representate their movement including their coded function:

Linear without easing:

float Linear::easeNull(float t, float b, float c, float d)
{
	return c * t / d + b;
}

Quadratic with ease in:

float Quad::easeIn(float t, float b, float c, float d)
{
	t /= d;
	return c * t*t + b;
}

Quadratic with ease out:

float Quad::easeOut(float t, float b, float c, float d)
{
	t /= d;
	return -c * t*(t - 2) + b;
}

Quadratic with ease in and out:

float Quad::easeInOut(float t, float b, float c, float d)
{
	t /= d / 2;
	if (t < 1) {
		return c / 2 * t*t + b;
	}
	t--;
	return -c / 2 * (t*(t - 2) - 1) + b;
}

Cubic with ease in:

float Cubic::easeIn(float t, float b, float c, float d)
{
	t /= d;
	return c * t*t*t + b;
}

Cubic with ease out:

float Cubic::easeOut(float t, float b, float c, float d)
{
	t /= d;
	t--;
	return c * (t*t*t + 1) + b;
}

Cubic with ease in and out:

float Cubic::easeInOut(float t, float b, float c, float d)
{
	t /= d / 2;
	if (t < 1) {
		return c / 2 * t*t*t + b;
	}
	t -= 2;
	return c / 2 * (t*t*t + 2) + b;
}

Quartic with ease in:

float Quart::easeIn(float t, float b, float c, float d)
{
	t /= d;
	return c * t*t*t*t + b;
}

Quartic with ease out:

float Quart::easeOut(float t, float b, float c, float d)
{
	t /= d;
	t--;
	return -c * (t*t*t*t - 1) + b;
}

Quartic with ease in and out:

float Quart::easeInOut(float t, float b, float c, float d)
{
	t /= d / 2;
	if (t < 1) return c / 2 * t*t*t*t + b;
	t -= 2;
	return -c / 2 * (t*t*t*t - 2) + b;
}

Quintic with ease in:

float Quint::easeIn(float t, float b, float c, float d)
{
	t /= d;
	return c * t*t*t*t*t + b;
}

Quintic with ease out:

float Quint::easeOut(float t, float b, float c, float d)
{
	t /= d;
	t--;
	return c * (t*t*t*t*t + 1) + b;
}

Quintic with ease in and out:

float Quint::easeInOut(float t, float b, float c, float d)
{
	t /= d / 2;
	if (t < 1) return c / 2 * t*t*t*t*t + b;
	t -= 2;
	return c / 2 * (t*t*t*t*t + 2) + b;
}

Sinusoidal with ease in:

float Sine::easeIn(float t, float b, float c, float d) {
	return -c * cos(t / d * (PI / 2)) + c + b;
}

Sinusoidal with ease out:

float Sine::easeOut(float t, float b, float c, float d) {
	return c * sin(t / d * (PI / 2)) + b;
}

Sinusoidal with ease in and out:

float Sine::easeInOut(float t, float b, float c, float d) {
	return -c / 2 * (cos(PI*t / d) - 1) + b;
}

Exponential with ease in:

float Expo::easeIn(float t, float b, float c, float d) {
	return c * pow(2, 10 * (t / d - 1)) + b;
}

Exponential with ease out:

float Expo::easeOut(float t, float b, float c, float d) {
	return c * (-pow(2, -10 * t / d) + 1) + b;
}

Exponential with ease in and out:

float Expo::easeInOut(float t, float b, float c, float d) {
	t /= d / 2;
	if (t < 1) return c / 2 * pow(2, 10 * (t - 1)) + b;
	t--;
	return c / 2 * (-pow(2, -10 * t) + 2) + b;
}

Circular with ease in:

float Circ::easeIn(float t, float b, float c, float d) {
	t /= d;
	return -c * (sqrt(1 - t * t) - 1) + b;
}

Circular with ease out:

float Circ::easeOut(float t, float b, float c, float d) {
	t /= d;
	t--;
	return c * sqrt(1 - t * t) + b;
}

Circular with ease in and out:

float Circ::easeInOut(float t, float b, float c, float d) {
	t /= d / 2;
	if (t < 1) return -c / 2 * (sqrt(1 - t * t) - 1) + b;
	t -= 2;
	return c / 2 * (sqrt(1 - t * t) + 1) + b;
}

Back with ease in:

float Back::easeIn(float t, float b, float c, float d) {
	float s = 1.70158;
	return c * (t /= d)*t*((s + 1)*t - s) + b;
}

Back with ease out:

float Back::easeOut(float t, float b, float c, float d) {
	float s = 1.70158;
	return c * ((t = t / d - 1)*t*((s + 1)*t + s) + 1) + b;
}

Back with ease in and out:

float Back::easeInOut(float t, float b, float c, float d) {
	float s = 1.70158f;
	if ((t /= d / 2) < 1) return c / 2 * (t*t*(((s *= (1.525)) + 1)*t - s)) + b;
	return c / 2 * ((t -= 2)*t*(((s *= (1.525)) + 1)*t + s) + 2) + b;
}

Elastic with ease in:

float Elastic::easeIn(float t, float b, float c, float d) {
	if (t == 0)
		return b;
	if ((t /= d) == 1)
		return b + c;
	float p = d * .3f;
	float a = c;
	float s = p / 4;
	return -(a * pow(2, 10 * (t -= 1)) * sin((t * d - s) * (2 * PI) / p)) + b;
}

Elastic with ease out:

float Elastic::easeOut(float t, float b, float c, float d) {
	if (t == 0) return b;
	if ((t /= d) == 1) return b + c;
	float p = d * .3f;
	float a = c;
	float s = p / 4;
	return (a*pow(2, -10 * t) * sin((t*d - s)*(2 * PI) / p) + c + b);
}

Elastic with ease in and out:

float Elastic::easeInOut(float t, float b, float c, float d) {
	if (t == 0)
		return b;
	if ((t /= d / 2) == 2)
		return b + c;
	float p = d * (.3f * 1.5f);
	float a = c;
	float s = p / 4;
	if (t < 1)
		return -.5f * (a * pow(2, 10 * (t -= 1)) * sin((t * d - s) * (2 * PI) / p)) + b;
	return a * pow(2, -10 * (t -= 1)) * sin((t * d - s) * (2 * PI) / p) * .5f + c + b;
}

Bounce with ease in:

float Bounce::easeIn(float t, float b, float c, float d) {
	return c - Bounce::easeOut(d - t, 0, c, d) + b;
}

Bounce with ease out:

float Bounce::easeOut(float t, float b, float c, float d) {
	if ((t /= d) < (1 / 2.75)) {
		return c * (7.5625*t*t) + b;
	}
	else if (t < (2 / 2.75)) {
		return c * (7.5625*(t -= (1.5 / 2.75))*t + .75) + b;
	}
	else if (t < (2.5 / 2.75)) {
		return c * (7.5625*(t -= (2.25 / 2.75))*t + .9375) + b;
	}
	else {
		return c * (7.5625*(t -= (2.625 / 2.75))*t + .984375) + b;
	}
}

Bounce with ease in and out:

float Bounce::easeInOut(float t, float b, float c, float d) {
	if (t < d / 2) return Bounce::easeIn(t * 2, 0, c, d) * .5 + b;
	return Bounce::easeOut(t * 2 - d, 0, c, d) * .5 + c * .5 + b;
}

Splines

From a mathematical point of view, a spline is a curve that appears as a result of a function defined in parts by polynomials. Splines are commonly used in programming because they are easy to build and accurate besides their capability of aproximating complex shapes through an interactive curve design. A spline is built through various control points that define their slope and follows diverese knots.

There are a lot of different types of splines but here only the most common ones will be shown:

Catmull-Rom Spline: is a type of cardinal splines that is continuous and the curve passes through all of the control points. It was formulated by Edwin Catmull and Raphael Rom.

Cubic Hermite Spline: is a spline where each piece is a third degree polynomial, just like any Cubic Spline, and it’s defined by its values and first derivatives at the end points, also called Hermite form. It’s named after Charles Hermite.

Linear Spline: is a continuous function defined by linear polynomials, which essentially means that is a continuous set of straight lines.

B-Spline (Basic Spline): it’s a spline defined as a linear combination of control points that has a minimal support given a degree, smoothness and domain. This spline is commonly used because it allows to express any spline of a certain degree by a linear combination of B-Splines of that degree. The term B-Spline was defined by Isaac Jacob Schoenberg.

NURBS (Non-uniform rational B-Spline): is a mathematical model commonly used in computer graphics for generating and representing curves and surfaces. It is a type of B-spline that offers great flexibility and precision for handling both analytic (in mathematical form) and modeled shapes.

Bézier Spline: is a continous splines defined picewise by different Bézier curves.

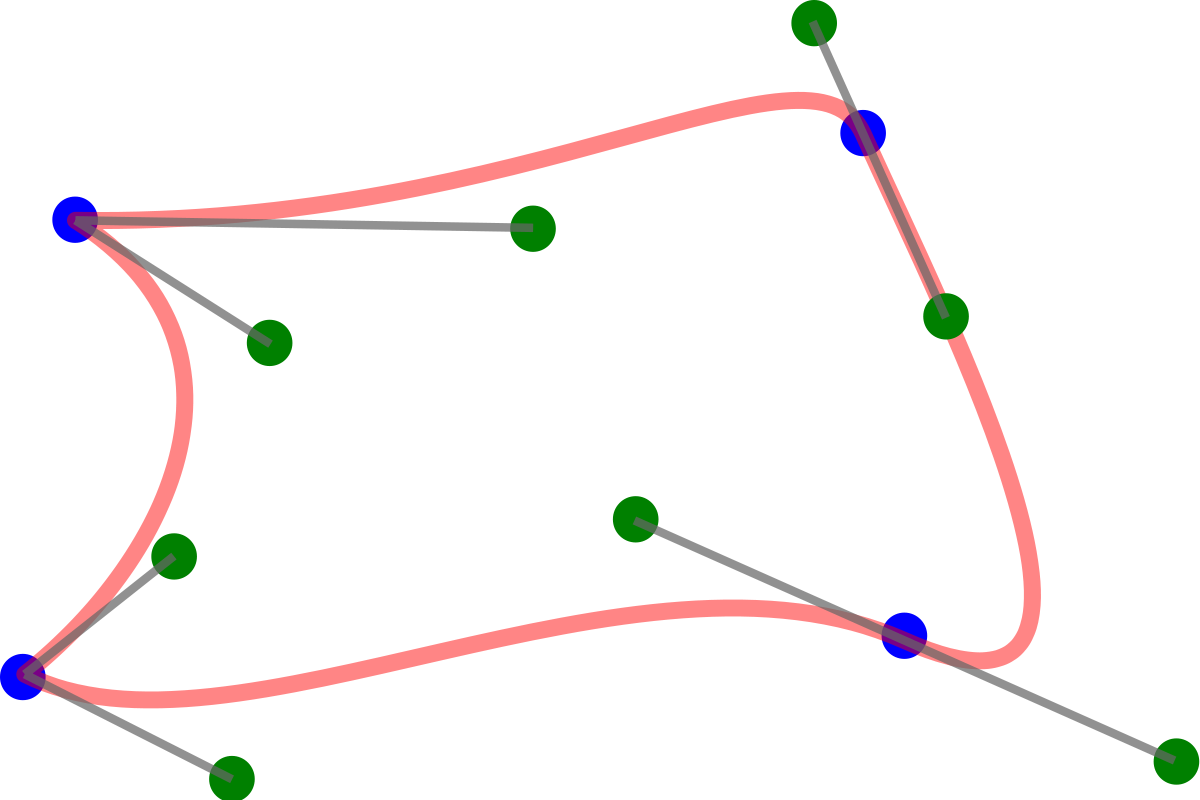
Splines Usability

The main usage of splines in videogames are to create paths for the enemies to follow. These paths should be continuous to have a smooth motion and this is exactly what a spline has to offer. In addition, any game that requires the player to level up can take use of splines to define the necessary experience needed increasingly between levels.

A great example of how a spline defines the motion of a camera in 2D videogames is the game Sonic the hedgehog. Even though it also takes into account the position of the player all the loops and transitions inside the level itself are created through a spline.

In 3D and VR videogames splines take a great importance in camera views, allowing the camera to move from a First Person point of view. A great example of this phenomenon is a simple rollercoaster where, if the camera follows the spline, the user can experience the view as if he were on that rollercoaster. Here there’s a video example of how a 3D camera following a spline creates a more realistic view:

Possible improvements on the system

Besides the implementation of the camera following a spline which I didn’t achieve because I felt overwhelmed by the mathematics it envolves, down below there are some improvements my system need:

Having a more accurate value of the panning with easing functions because, as far as the camera works with integer values and the easing functions return values with decimals, a little part of the movement is lost on each iteration making the panning end not where it is supposed to.
Polishing my easingBetweenPoints function so it supports more tweens, currently it only supports any of the EaseOut functions.
Cleaning up my code and creating the functions in a separate class and not inside the scene module.
Creating the easing library as a defined static library instead of a source and header file, which I had actually done but had some stupid error that made me create a new project to then have to fix the error myself.
Creating an interpolation class to be able to handle splines to then implement the camera movement following that custom spline.
Adding an exercise solution so any developer can understand my code and implement it to their own project.